Definisi Teorema Bayes
Apa itu Teorema Bayes?
teorema Bayes, dinamai setelah ahli matematika Inggris abad ke-18 Thomas Bayes, adalah rumus matematika untuk menentukan probabilitas bersyarat. Probabilitas bersyarat adalah kemungkinan hasil yang terjadi, berdasarkan hasil sebelumnya yang terjadi. Teorema Bayes menyediakan cara untuk merevisi prediksi atau teori yang ada (memperbarui probabilitas) yang diberikan bukti baru atau tambahan. Di bidang keuangan, Teorema Bayes dapat digunakan untuk menilai risiko meminjamkan uang kepada calon peminjam.
Teorema Bayes juga disebut Aturan Bayes atau Hukum Bayes dan merupakan dasar dari bidang statistik Bayesian.
Takeaways Kunci
- Teorema Bayes memungkinkan Anda untuk memperbarui probabilitas yang diprediksi dari suatu peristiwa dengan memasukkan informasi baru.
- Teorema Bayes dinamai sesuai dengan matematikawan abad ke-18 Thomas Bayes.
- Hal ini sering digunakan di bidang keuangan dalam memperbarui evaluasi risiko.
Memahami Teorema Bayes
Aplikasi teorema tersebar luas dan tidak terbatas pada bidang keuangan. Sebagai contoh, Teorema Bayes dapat digunakan untuk menentukan keakuratan hasil tes medis dengan mempertimbangkan seberapa besar kemungkinan seseorang terkena penyakit dan akurasi tes secara umum. Teorema Bayes bergantung pada penggabungan distribusi probabilitas sebelumnya untuk menghasilkan probabilitas posterior. Probabilitas sebelumnya, dalam inferensi statistik Bayesian, adalah probabilitas suatu peristiwa sebelum data baru dikumpulkan. Ini adalah penilaian rasional terbaik dari kemungkinan hasil berdasarkan pengetahuan saat ini sebelum percobaan dilakukan. Probabilitas posterior adalah probabilitas yang direvisi dari suatu peristiwa yang terjadi setelah mempertimbangkan informasi baru. Probabilitas posterior dihitung dengan memperbarui probabilitas sebelumnya dengan menggunakan teorema Bayes. Dalam istilah statistik, Probabilitas posterior adalah peluang terjadinya kejadian A jika kejadian B telah terjadi.
Teorema Bayes dengan demikian memberikan probabilitas suatu peristiwa berdasarkan informasi baru yaitu, atau mungkin terkait, ke acara itu. Rumus tersebut juga dapat digunakan untuk melihat bagaimana kemungkinan terjadinya suatu peristiwa dipengaruhi oleh informasi baru yang bersifat hipotetis, seandainya informasi baru itu ternyata benar. Contohnya, katakanlah satu kartu diambil dari setumpuk penuh 52 kartu. Peluang terambilnya kartu adalah raja adalah empat dibagi 52, yang sama dengan 1/13 atau sekitar 7,69%. Ingatlah bahwa ada empat raja di geladak. Sekarang, misalkan terungkap bahwa kartu yang dipilih adalah kartu wajah. Peluang kartu yang terpilih adalah raja, mengingat itu adalah kartu wajah, adalah empat dibagi 12, atau sekitar 33,3%, karena ada 12 kartu wajah dalam satu dek.
Rumus Teorema Bayes
Contoh Teorema Bayes
Di bawah ini adalah dua contoh teorema Bayes di mana contoh pertama menunjukkan bagaimana rumus dapat diturunkan dalam contoh investasi saham menggunakan Amazon.com Inc. (AMZN). Contoh kedua menerapkan teorema Bayes untuk pengujian obat farmasi.
Menurunkan Rumus Teorema Bayes
Teorema Bayes hanya mengikuti aksioma probabilitas bersyarat. Probabilitas bersyarat adalah probabilitas suatu peristiwa mengingat bahwa peristiwa lain terjadi. Sebagai contoh, pertanyaan probabilitas sederhana mungkin bertanya:"Berapa probabilitas jatuhnya harga saham Amazon.com?" Probabilitas bersyarat membawa pertanyaan ini selangkah lebih maju dengan menanyakan:"Berapa probabilitas jatuhnya harga saham AMZN? mengingat bahwa indeks Dow Jones Industrial Average (DJIA) turun lebih awal?"
Probabilitas bersyarat A jika B telah terjadi dapat dinyatakan sebagai:
Jika A adalah:"Harga AMZN turun" maka P(AMZN) adalah probabilitas bahwa AMZN turun; dan B adalah:"DJIA sudah down, " dan P(DJIA) adalah probabilitas bahwa DJIA jatuh; maka ekspresi probabilitas bersyarat berbunyi sebagai "probabilitas bahwa AMZN turun karena penurunan DJIA sama dengan probabilitas bahwa harga AMZN turun dan DJIA menurun atas probabilitas penurunan indeks DJIA.
P(AMZN|DJIA) =P(AMZN dan DJIA) / P(DJIA)
P(AMZN dan DJIA) adalah peluang dari keduanya A dan B terjadi. Ini juga sama dengan probabilitas terjadinya A dikalikan dengan probabilitas B terjadi jika A terjadi, dinyatakan sebagai P(AMZN) x P(DJIA|AMZN). Fakta bahwa kedua ekspresi ini sama mengarah ke teorema Bayes, yang ditulis sebagai:
jika, P(AMZN dan DJIA) =P(AMZN) x P(DJIA|AMZN) =P(DJIA) x P(AMZN|DJIA)
kemudian, P(AMZN|DJIA) =[P(AMZN) x P(DJIA|AMZN)] / P(DJIA).
Dimana P(AMZN) dan P(DJIA) adalah probabilitas jatuhnya Amazon dan Dow Jones, tanpa memperhatikan satu sama lain.
Rumus tersebut menjelaskan hubungan antara probabilitas hipotesis sebelum melihat bukti bahwa P(AMZN), dan probabilitas hipotesis setelah mendapatkan bukti P(AMZN|DJIA), diberikan hipotesis untuk Amazon diberikan bukti di Dow.
Contoh Numerik Teorema Bayes
Sebagai contoh numerik, bayangkan ada tes narkoba yang 98% akurat, artinya 98% dari waktu menunjukkan hasil positif yang sebenarnya untuk seseorang yang menggunakan narkoba dan 98% dari waktu menunjukkan hasil yang benar-benar negatif untuk bukan pengguna narkoba. Lanjut, asumsikan 0,5% orang menggunakan obat. Jika seseorang yang dipilih secara acak tes positif untuk obat, perhitungan berikut dapat dilakukan untuk melihat apakah probabilitas orang tersebut benar-benar pengguna narkoba.
(0,98 x 0,005) / [(0,98 x 0,005) + ((1 - 0,98) x (1 - 0,005))] =0,0049 / (0,0049 + 0,0199) =19,76%
Teorema Bayes menunjukkan bahwa bahkan jika seseorang dites positif dalam skenario ini, sebenarnya jauh lebih mungkin orang tersebut bukan pengguna narkoba.
Keuangan
-
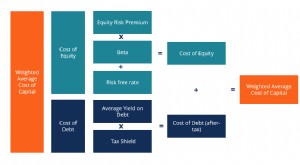 Definisi WACC
Definisi WACC Biaya Modal Rata-Rata Tertimbang (WACC) perusahaan mewakili biaya modal campurannya Biaya Modal Biaya modal adalah tingkat pengembalian minimum yang harus diperoleh bisnis sebelum menghasilkan nilai. ...
-
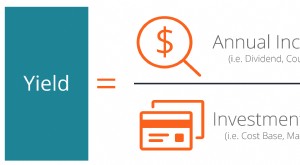 Apa itu Hasil (Definisi)?
Apa itu Hasil (Definisi)? Yield didefinisikan sebagai laba atas investasi hanya pendapatan (tidak termasuk capital gainCapital Gains YieldCapital gainyield (CGY) adalah apresiasi harga atas investasi atau sekuritas yang dinyat...