Apa itu Pertumbuhan Eksponensial?

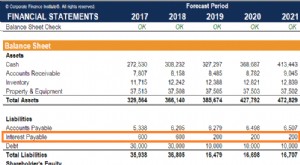
Pertumbuhan eksponensial adalah ketika data naik selama periode waktu tertentu, menciptakan kurva tren naik pada grafik. Dalam matematika, ketika fungsi menyertakan kekuatan (atau eksponen), perhitungan akan meningkat secara eksponensial. Sebagai contoh, jika ayam bertelur tiga kali setahun dan tiga kali lipat setiap tahun, kemudian pada tahun kedua, akan ada 27, dan pada tahun ketiga, akan ada 81.

Ringkasan

• Pertumbuhan eksponensial dapat diilustrasikan sebagai grafik yang awalnya datar dan secara instan tumbuh dalam arah vertikal selama periode waktu tertentu.
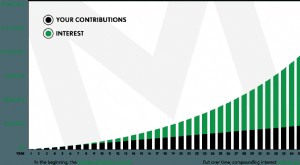
• Dalam bidang keuangan, pertumbuhan eksponensial sebagian besar terlihat pada bunga majemuk, yang lazim di berbagai instrumen investasi, termasuk saham dan rekening tabungan berbunga tinggi.
• Bunga majemuk menguntungkan bagi investor, karena mereka dapat meningkatkan kekayaan bersih mereka dari waktu ke waktu menggunakan sejumlah kecil arus kas.

Memahami Pertumbuhan Eksponensial

Dalam bidang keuangan, ketika seorang individu menyimpan uang dalam rekening tabungan hasil tinggi Rekening TabunganA rekening tabungan adalah rekening khas di bank atau serikat kredit yang memungkinkan seorang individu untuk menyimpan, aman, atau menarik uang ketika dibutuhkan. Rekening tabungan biasanya membayar beberapa bunga deposito, meskipun tarifnya cukup rendah. untuk jangka waktu yang lama, investor akan menerima pengembalian majemuk karena pertumbuhan eksponensial. Ini adalah contoh bagaimana investasi dapat tumbuh secara eksponensial dengan pengeluaran awal yang kecil.

Jika akun memberikan tingkat bunga majemuk, maka investor akan menerima bunga atas pokok dan pembayaran bunga yang diterima dari periode sebelumnya. Sebagai contoh, di tahun pertama, investor dapat menerima bunga 15% pada obligasi nilai nominal $100 yang jatuh tempo dalam 30 tahun. Karena itu, dia akan menerima $15.

Pada tahun kedua, tingkat bunga 15% kemudian akan diterapkan ke $115 daripada $100, mempertimbangkan pembayaran bunga yang diberikan pada tahun pertama. Dengan demikian, karena setiap tahun berlalu, pembayaran bunga akan terus terakumulasi dan dipertimbangkan dalam perhitungan pembayaran bunga tahunan pada saat instrumen keuangan jatuh tempo. Jika diilustrasikan, pertumbuhan akan menjadi kurva eksponensial.

Rumus Pertumbuhan Eksponensial

Secara ilustrasi, grafik eksponensial akan mulai rendah dan tampak datar untuk beberapa waktu sebelum meningkat hampir ke arah vertikal. Hal itu dapat dirasakan sebagai berikut:

V =S * (1+r)^T

Di mana:

• S =Nilai awal atau jumlah pokok
• R =Tingkat pengembalian (atau tingkat bunga)
• T =Waktu yang telah berlalu sejak penerbitan instrumen keuangan

Memahami Apa Itu Peracikan

Kepada investor, peracikan berarti kemampuan untuk menumbuhkan kekayaan seseorang secara eksponensial selama periode waktu tertentu dengan memperoleh bunga atas pendapatan tambahan yang diterima dari pembayaran bunga sebelumnya yang berasal dari jumlah pokok. Ini kontras dengan bunga sederhanaSimple InterestSimple interestrumus, definisi dan contohnya. Bunga sederhana adalah perhitungan bunga yang tidak memperhitungkan efek pemajemukan. Dalam banyak kasus, bunga majemuk dengan setiap periode pinjaman yang ditentukan, tetapi dalam kasus kepentingan sederhana, itu tidak. Perhitungan bunga sederhana sama dengan jumlah pokok dikalikan dengan tingkat bunga, dikalikan dengan jumlah periode., karena tidak mencerminkan peracikan. Bunga sederhana hanya membayar bunga pada pokok asli, tidak termasuk pendapatan yang diterima selama umur instrumen keuangan.

Untuk menghitung bunga majemuk, rumusnya adalah sebagai berikut:

P[(1+i)^n-1]

Di mana:

• P =Kepala Sekolah
• Saya =Tingkat bunga tahunan nominal
• n =Jumlah periode peracikan

Penggunaan Pertumbuhan Eksponensial

Pertumbuhan eksponensial sering digunakan dalam pemodelan keuanganPemodelan KeuanganSumber daya pemodelan keuangan gratis dan panduan untuk mempelajari konsep yang paling penting dengan kecepatan Anda sendiri. Artikel ini akan mengajarkan Anda praktik terbaik pemodelan keuangan dengan ratusan contoh, template, panduan, artikel, dan banyak lagi. Pelajari apa itu pemodelan keuangan, cara membuat model, keterampilan Excel, tips dan trik. Meskipun konsepnya terlihat jelas dalam rekening tabungan berbunga tinggi, alasannya adalah karena suku bunga cenderung tidak goyah atau berfluktuasi sebanyak selama keadaan ekonomi yang berbeda. Namun, dalam mempertimbangkan saham, pengembalian tidak mulus.

Keseluruhan, model pertumbuhan eksponensial berguna dalam memprediksi pengembalian investasi ketika tingkat pertumbuhan stabil dan tidak sering berosilasi.

Lebih Banyak Sumber Daya

CFI menawarkan Halaman Program Capital Markets &Securities Analyst (CMSA)® - CMSADaftar dalam program CMSA® CFI dan menjadi Analis Pasar Modal &Sekuritas bersertifikat. Tingkatkan karir Anda dengan program dan kursus sertifikasi kami. program sertifikasi bagi mereka yang ingin membawa karir mereka ke tingkat berikutnya. Untuk terus belajar dan memajukan karir Anda, sumber daya berikut akan membantu:

• Pengembalian Majemuk Berkelanjutan Pengembalian Majemuk Berkelanjutan Pengembalian Majemuk Berkelanjutan adalah apa yang terjadi ketika bunga yang diperoleh dari suatu investasi dihitung dan diinvestasikan kembali ke dalam rekening untuk jangka waktu yang tidak terbatas. Bunga dihitung dari jumlah pokok dan bunga yang terakumulasi selama periode tertentu
• Tingkat Bunga Tahunan Efektif Tingkat Bunga Tahunan Efektif Tingkat Bunga Tahunan Efektif (EAR) adalah tingkat bunga yang disesuaikan untuk peracikan selama periode tertentu. Sederhananya, yang efektif
• Tingkat PengembalianTingkat PengembalianTingkat Pengembalian (ROR) adalah keuntungan atau kerugian dari suatu investasi selama periode waktu yang dibandingkan dengan biaya awal investasi yang dinyatakan dalam persentase. Panduan ini mengajarkan formula yang paling umum
• Tingkat Pertumbuhan Majemuk Tingkat Pertumbuhan MajemukLaju pertumbuhan majemuk adalah ukuran yang digunakan secara khusus dalam konteks bisnis dan investasi, yang menunjukkan tingkat pertumbuhan selama beberapa periode waktu. Ini adalah ukuran pertumbuhan konstan dari seri data. Keuntungan terbesar dari tingkat pertumbuhan majemuk adalah bahwa metrik mempertimbangkan efek peracikan.